Landmåling/Beregning af afstand mellem to punkter

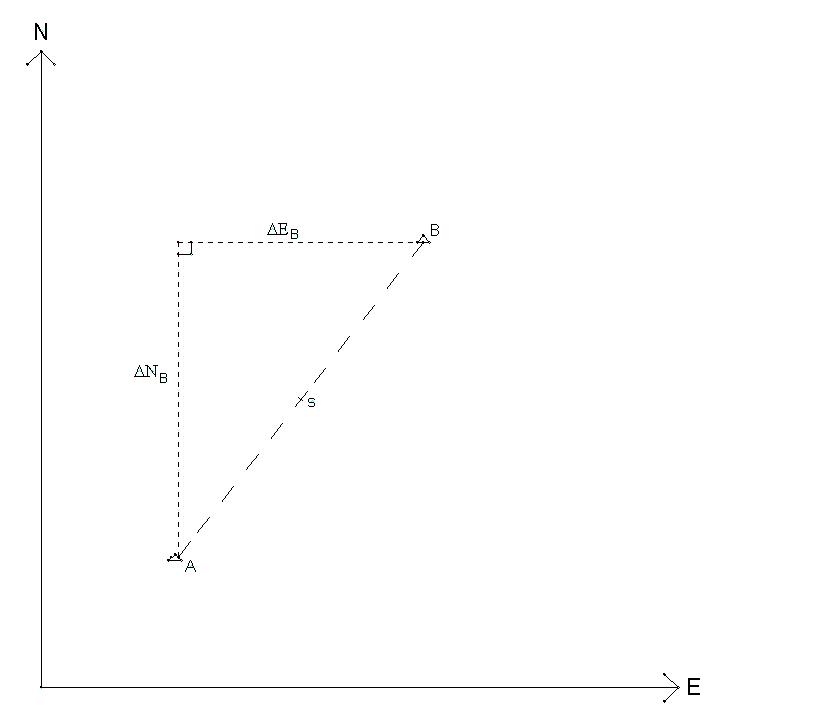
Jævnligt har man behov for at beregne afstanden mellem to punkter, hvortil der findes koordinater. Beregningen tager udgangspunkt i Pythagoras’ sætning, jvf. nedenstående figur.

Vi ønsker at beregne afstanden mellem punkt A og B, dvs. længden s, som er hypotenusen i den retvinklede trekant.

Pythagoras sætning på ovennævnte trekant lyder: $s=\sqrt{\mathrm{\Delta }{N}^2+\mathrm{\Delta }{E}^2}$

Trekantens ene katete $\mathrm{\Delta }N$ er forskellen mellem punkt A og punkt B's Northing-koordinater ($N_B-N_A$). Trekantens anden katete $\mathrm{\Delta }E$ er forskellen mellem punkt A og punkt B's Easting-koordinater ($E_B-E_A$). Derfor kan formlen omskrives til følgende afstandsformel:

$s=\sqrt{(N_B-N_A{)}^2+(E_B-E_A{)}^2}$

Afstanden mellem to punkter kan altså beregnes, når man kender punkternes Northing og Easting-koordinater.

Bemærk, at da parenteserne opløftes i 2., er det uden betydning hvilket punkt, der kaldes A og B. Endvidere bemærkes det, at såfremt man bruger System-34, kan Northing og Easting-koordinaterne direkte erstattes med Y- og X-koordinater.

Eksempel

Afstanden ønskes beregnet mellem punkterne A og B. Punkterne har følgende koordinater:

Punkt	N	E
A	137,15	219,32
B	319,23	412,19

Koordinaterne sættes ind i ovenstående formel:

$s=\sqrt{(319,23-137,15{)}^2+(412,19-219,32{)}^2}=265,24m$

Det vil sige, at der er 265,24 m mellem punkt A og B.

Denne formel vil vi ofte bruge i de følgende beregninger.