Landmåling/En fri opstilling

Beregning af en fri opstilling i UTM

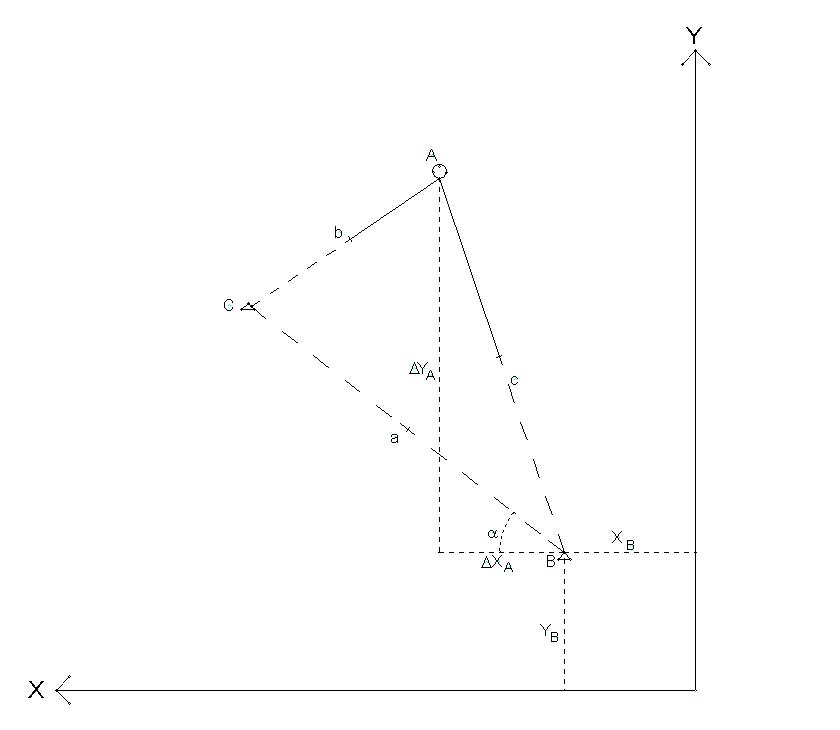
På ovennævnte skitse er totalstationen opstillet et tilfældigt sted i punkt A. Koordinaterne til punkt A beregnes ved, at der måles både afstand og retning til punkt A og B, som er to kendte punkter.

Først beregnes $\mathrm{\angle }A$ ved at trække retningen mod punkt C fra retninen mod punkt B - dvs.:

$\mathrm{\angle }A=r_C-r_B$

Afstanden a beregnes derefter ud fra koordinaterne til punkt B og C ved hjælp af afstandsformlen:

$a=\sqrt{(N_C-N_B{)}^2+(E_C-E_B{)}^2}$

Retningsvinklen fra punkt B til C beregnes herefter ud fra følgende formel:

$\alpha ={\tan }^{-1}\left(\frac{E_C-E_B}{N_C-N_B}\right)$.

$\mathrm{\angle }B$ skal herefter beregnes. Dette gør vi indirekte ved at beregne $\mathrm{\angle }C$, hvorefter $\mathrm{\angle }B$ kan beregnes. $\mathrm{\angle }C$ beregnes ved hjælp af sinusrelationen.

$\mathrm{\angle }C={\sin }^{-1}\left(\frac{c*\sin A}{a}\right)$.

$\mathrm{\angle }B$ beregnes herefter vha. følgende formel:

$\mathrm{\angle }B=200-\mathrm{\angle }A-\mathrm{\angle }C$.

Punkt A's koordinater kan nu beregnes ud fra følgende formler: $N_A=\cos (\alpha +\mathrm{\angle }B)*c+N_B$

$E_A=\sin (\alpha +\mathrm{\angle }B)*c+E_B$

Eksempel

Der er målt en fri opstilling med følgende observationer:

Observationer:	Opst. i punkt A
Pkt.	retning	vandret afstand
B	3,173	263,043
C	90,368	-

Koordinater:
Pkt.	N	E
B	137,15	219,32
C	319,23	412,19

Vinkel A kan beregnes ud fra de to retninger:

$\mathrm{\angle }A=90,368-3,173=87,195gon$

Afstanden mellem punkt B og C:

$a=\sqrt{(319,23-137,15{)}^2+(412,19-219,32{)}^2}=265,24m$

Retningsvinklen fra B mod C:

$\alpha ={\tan }^{-1}\left(\frac{412,19-219,32}{319,23-137,15}\right)=51,832gon$

Det ses, at både tæller og nævner er positive, hvorfor der skal lægges 0 gon til retningsvinklen, som så bliver:

$\alpha =51,832gon$

Vinkel B bliver herefter:

$\mathrm{\angle }C={\sin }^{-1}\left(\frac{263,043*\sin (87,195)}{265,24}\right)=84,822gon$

$\mathrm{\angle }B=200-87,195-84,822=27,983gon$

A's koordinater bliver hermed:

$N_A=\cos (51,832+27,972)*263,043+137,15=219,20m$

$E_A=\sin (51,832+27,972)*263,043+219,32=469,24m$

Beregning af en fri opstilling i System-34

På ovennævnte skitse er totalstationen opstillet et tilfældigt sted i punkt A. Koordinaterne til punkt A beregnes ved, at der måles både afstand og retning til punkt A og B, som er to kendte punkter.

Først beregnes $\mathrm{\angle }A$ ved at trække retningen mod punkt C fra retninen mod punkt B - dvs.:

$\mathrm{\angle }A=r_C-r_B$

Afstanden a beregnes derefter ud fra koordinaterne til punkt B og C ved hjælp af afstandsformlen:

$a=\sqrt{(Y_C-Y_B{)}^2+(X_C-X_B{)}^2}$

Retningsvinklen fra punkt B til C beregnes herefter ud fra følgende formel:

$\alpha ={\tan }^{-1}\left(\frac{Y_C-Y_B}{X_C-X_B}\right)$.

$\mathrm{\angle }B$ skal herefter beregnes. Dette gør vi indirekte ved at beregne $\mathrm{\angle }C$, hvorefter $\mathrm{\angle }B$ kan beregnes. $\mathrm{\angle }C$ beregnes ved hjælp af sinusrelationen.

$\mathrm{\angle }C={\sin }^{-1}\left(\frac{c*\sin A}{a}\right)$.

$\mathrm{\angle }B$ beregnes herefter vha. følgende formel:

$\mathrm{\angle }B=200-\mathrm{\angle }A-\mathrm{\angle }C$.

Punkt A's koordinater kan nu beregnes ud fra følgende formler: $Y_A=\sin (\alpha +\mathrm{\angle }B)*c+Y_B$

$X_A=\cos (\alpha +\mathrm{\angle }B)*c+X_B$

Eksempel

Der er målt en fri opstilling med følgende observationer:

Observationer:	Opst. i punkt A
Pkt.	retning	vandret afstand
B	3,173	263,043
C	90,368	-

Koordinater:
Pkt.	Y	X
B	219,32	137,15
C	412,19	319,23

Vinkel A kan beregnes ud fra de to retninger:

$\mathrm{\angle }A=90,368-3,173=87,195gon$

Afstanden mellem punkt B og C:

$a=\sqrt{(319,23-137,15{)}^2+(412,19-219,32{)}^2}=265,24m$

Retningsvinklen fra B mod C:

$\alpha ={\tan }^{-1}\left(\frac{412,19-219,32}{319,23-137,15}\right)=51,832gon$

Det ses, at både tæller og nævner er positive, hvorfor der skal lægges 0 gon til retningsvinklen, som så bliver:

$\alpha =51,832gon$

Vinkel B bliver herefter:

$\mathrm{\angle }C={\sin }^{-1}\left(\frac{263,043*\sin (87,195)}{265,24}\right)=84,822gon$

$\mathrm{\angle }B=200-87,195-84,822=27,983gon$

A's koordinater bliver hermed:

$Y_A=\sin (51,832+27,972)*263,043+219,32=469,24m$

$X_A=\cos (51,832+27,972)*263,043+137,15=219,20m$

I dette eksempel er der målt det absolut minimum af observationer. Målingen er kun bestemt. Dermed vil en evt. grov fejl i observationerne ikke kunne opdages i beregningerne. I praksis vil man altid forsøge at indmålte retninger og afstande til mindst 3 punkter således, at den frie opstilling er overbestemt. Dermed vil man kunne kombinere de forskellige observationer på forskellig vis i beregningerne - med tre kendte punkter kan der dannes 3 vinkårlige trekanter, hvori opstillingspunktet indgår. Dette vil medfører - såfremt der ikke er grove fejl i observationerne - at de beregnede koordinater til punt A vil blive de samme inden for målenøjagtigheden uanset hvilke observationer, der kombineres.

I dette tilfælde vil det bedste koordinatsæt til punkt A være gennemsnittet af de beregnede koordinater ud fra de 3 vilkårlige trekanter. Der findes også beregningsmetoder, hvor man på en gang kan beregne ét koordinatsæt til punkt A ud fra alle observationerne. Denne metode kaldes for udjævning.